swgr's Blog

[research] sampling

今天的group meeting延续了上周的话题，讲的是sampling（采样）。听得不是很明白。

--------------------------------------

假设我们要在分布y上采样，并且，假设所求的分布y可以表述为在标准分布z上施加一个操作f产生的，即 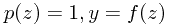$p(z) = 1, y = f(z)$

从概率密度函数(pdf)的定义出发，就有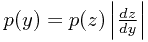 $p(y)=p(z)\left|{\frac{dz}{dy}}\right|$

把右边的微分乘到左边并且积分，就有

$z = h(y) = \int_{-\infty}^{y}p(\tilde{y})d\tilde{y}$

这样，就通过z把h和f建立起了关系，即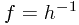 $f = h^{-1}$

这也就是说，假设我们能求出p(y)的cumulative density fucntion(累计密度函数)h(y)的反函数h^{-1}(y)，那也就是知道f了，这样，通过在z上均匀采样（由于z是一个标准分布，采样很容易），再经过y=f(z)变换，就能在y分布上均匀地采样了。

--------------------------------------

当然，以上是最简单的情况（所谓“直接法”）。但是实际上在sampling的时候，由于很难求出分布的方程p(y)，或者求出了cdf但是不好求反函数，或者所求的分布p(y)的范围太大不好积分，因此很难用上述办法来做。因此，采用了各种方法来进行sampling。

--------------------------------------

比如reject sampling的方法。思路是：

既然p(x)不好采样，我们搞一个比较容易采样的函数q(x)，并且乘上一个系数k让它保证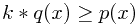 $k*q(x)\geq p(x)$

这样在kq(x)上采样即可。当然，这样采样的时候不总是能保证采样的结果是有效的，

因此如果采样的结果是落在p(x)内，就accept，落在p(x)到kq(x)直接，就reject。

这就是reject sampling的思路。这里需要考虑一个reject rate的问题，就是如果kq(x)太大了，那么就很难取到p(x)内的采样点，实际效果就是大部分的sampling都要reject掉，效率很低。因此kq(x)的选择要恰当。

常用的q(x)有Guassian Distribution、Cauthy Distribution，指数分布等等。

--------------------------------------

先写到这，后面的Importance sampling和MCMC没怎么听懂，基于MCMC的Particle Filtering以前倒是听过，有空找个时间学一下。

另外，写这篇日志的过程中学到一些Tex的语法..