swgr's Blog
[research] sampling
今天的group meeting延续了上周的话题,讲的是sampling(采样)。听得不是很明白。
--------------------------------------
假设我们要在分布y上采样,并且,假设所求的分布y可以表述为在标准分布z上施加一个操作f产生的,即 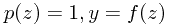
从概率密度函数(pdf)的定义出发,就有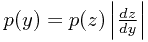
把右边的微分乘到左边并且积分,就有
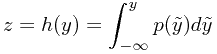
这样,就通过z把h和f建立起了关系,即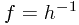
这也就是说,假设我们能求出p(y)的cumulative density fucntion(累计密度函数)h(y)的反函数h^{-1}(y),那也就是知道f了,这样,通过在z上均匀采样(由于z是一个标准分布,采样很容易),再经过y=f(z)变换,就能在y分布上均匀地采样了。
--------------------------------------
当然,以上是最简单的情况(所谓“直接法”)。但是实际上在sampling的时候,由于很难求出分布的方程p(y),或者求出了cdf但是不好求反函数,或者所求的分布p(y)的范围太大不好积分,因此很难用上述办法来做。因此,采用了各种方法来进行sampling。
--------------------------------------
比如reject sampling的方法。思路是:
既然p(x)不好采样,我们搞一个比较容易采样的函数q(x),并且乘上一个系数k让它保证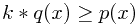
这样在kq(x)上采样即可。当然,这样采样的时候不总是能保证采样的结果是有效的,
因此如果采样的结果是落在p(x)内,就accept,落在p(x)到kq(x)直接,就reject。
这就是reject sampling的思路。这里需要考虑一个reject rate的问题,就是如果kq(x)太大了,那么就很难取到p(x)内的采样点,实际效果就是大部分的sampling都要reject掉,效率很低。因此kq(x)的选择要恰当。
常用的q(x)有Guassian Distribution、Cauthy Distribution,指数分布等等。
--------------------------------------
先写到这,后面的Importance sampling和MCMC没怎么听懂,基于MCMC的Particle Filtering以前倒是听过,有空找个时间学一下。
另外,写这篇日志的过程中学到一些Tex的语法..
[course] TCP Exploit
今天做了security课的assignment 2里的problem 2,是关于TCP Exploit的。
简单说,就是一个在基于广播的LAN中(比如HUB结构的LAN)干扰别人正常TCP连接的东西。
例如,A和B在通过TCP正常地通信,攻击者C想要中断这个通讯。
于是C通过抓包得知了A和B的通信端口,然后伪装成其中一方(比如A)像另一方(比如B)发一个TCP的FIN包。
这时,B就会以为A想跟它断开TCP通讯,于是就给A发了FIN包,一来二去双方就断开了。
值得注意的是:
1. C抓包的时候其实不止是为了得知A和B的通信端口,更重要的是得知通讯过程中的seq号,这样才能正确发出FIN包而不被B拒绝。
2. A最后会给B发FIN包(因为它收到了B给它发的FIN包,以为B想跟自己断开了),但是这个FIN包的seq是不会被B接受的(因为B收到过来自C的FIN包,它以为是A发的,因此导致了双方计算中seq的不一致),因此,最后B会给A发一个RST包。
闲的蛋疼,挑战一下Quine...
刚睡醒,比较闲,小玩一下...
main(a,b)
{
char c[1024];
a="public class Main \
{ \
public static void main(String[]args) \
{ \
String a=%%c%%s%%c; \
String b=%%c%%s%%c; \
String c=String.format(a); \
System.out.printf(c,34,b,34,34,a,34); \
}
}";
b="main(a,b) \
{ \
char c[1024]; \
a=%%c%%s%%c; \
b=%%c%%s%%c; \
sprintf(c,a); \
printf(c,34,b,34,34,a,34); \
}";
sprintf(c,a);
printf(c,34,b,34,34,a,34);
}
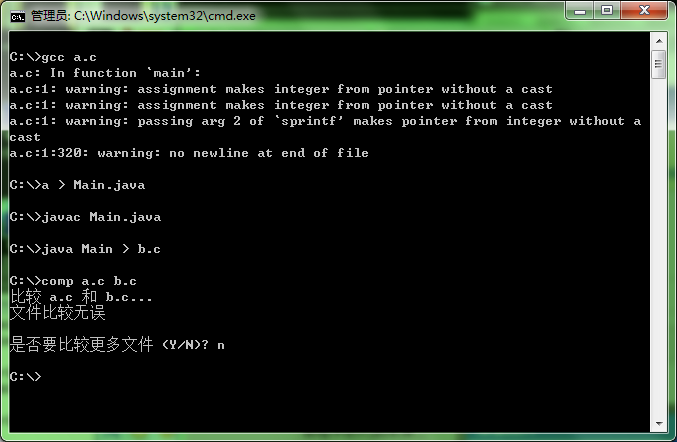
public class Main
{
public static void main(String[]args)
{
String a="main(a,b)
{
char c[1024];
a=%%c%%s%%c;
b=%%c%%s%%c;
sprintf(c,a);
printf(c,34,b,34,34,a,34);
}";
String b="public class Main
{
public static void main(String[]args)
{
String a=%%c%%s%%c;
String b=%%c%%s%%c;
String c=String.format(a);
System.out.printf(c,34,b,34,34,a,34);
}
}";
String c=String.format(a);
System.out.printf(c,34,b,34,34,a,34);
}
}
从经典的AOV网、AOE网想到的问题
晚上煮点心吃的时候,突然想到一个问题。
----------------------我是混个陷----------------------
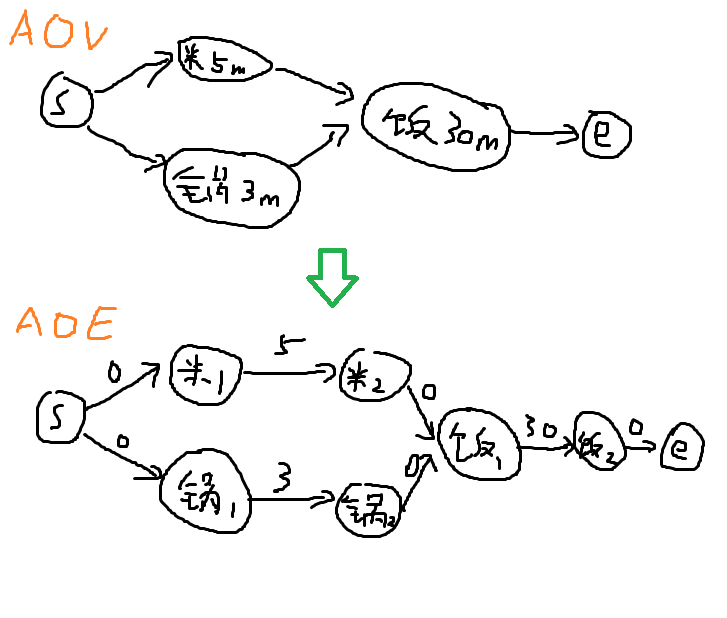
首先经典的工序问题的模型一般是,给出一个工程(比如做晚餐),包括工序之间的拓扑关系和每道工序所需要的时间。(比如洗米需要5min,洗锅需要3min,完成洗米、洗锅以后才能煮饭,煮饭需要30min...)
然后就可以在这个模型上做各种事了,譬如求一个可行的完成顺序(拓扑排序),或者求一个最短的完成时间(关键路径)等等。
----------------------还是混个陷----------------------
好吧,现在来说说我想到的问题。
在这个工序问题模型的基础上加入一个限制条件:同时进行的工序数不能超过m(可以理解为厨房一共有m个人在忙活)。显然,当m=1时,问题就变成了拓扑排序;当m=∞时,问题就变成了关键路径。
那么,当m不是1也不是无穷大时,如果想求工程的最短的完成时间,要如何做呢?
我还没有认真想这个问题的算法,我觉得某种类似关键路径的贪心方法可以做掉。
ACM_DIY群上有大牛无责任猜想是费用流做,不会网络流的菜鸟我表示压力很大。
----------------------就是混个陷----------------------
其实这里还涉及到一个如何把AOV网转成AOE网的问题。
以下是我无责任猜想的做法,不多说,直接上图。(鼠绘,渣技术,我自重)
搬家
找一个比较舒服的支持RSS和优秀Syntax Highlight的blog真不容易,汗。
就先住在这吧。
#include<stdio.h>
int main()
{
printf("hello, world\n");
return 0;
}